Təbiət elmləri ilə maraqlanmayan az adam tapmaq olar. Bu sahədə işləyənlərdən əlavə, elmi-kütləvi kitabları oxuyan, Youtube-da elmi kanalları izləyən çoxsaylı insanlar arasında sözsüz həmvətənlərimiz də var. Kvant Dünyası səhifəsi də bu məqsədə qulluq edir - elmi yaymaq. Artıq, qara dəliklər (qara çuxurlar) tez-tez rast gəldiyimiz məşhur ifadəyə çevrilib. Bu yazıda, onların maraqlı xassələrinə toxunacıq.
İşığın belə tərk edə bilməyəcəyi intensiv cəzbetmə sahəsinə malik ağır səma cisimlərinin varlığı barədə ilk olaraq 1784-cü ildə Con Mişel yazmışdı. Albert Eynşteynin ümumi nisbilik nəzəriyyəsinin önəmli təxminlərindən biri olmasına baxmayaraq, hələ ötən əsrin ikinci yarısınadək varlığı şübhə altında idi. Bilinən heç bir şeyin onun qravitasiyasından çıxmadığına görə birbaşa müşahidə etmək mümkün deyil. Lakin, alimlər, həmin qravitasiya sahəsinin ətrafda göstərəcəyi təsirlərə görə dolayı yollarla qara dəliklərin varlığını müşahidə etmişlər. Hal-hazırda qara dəlik olduğu güman edilən minlərlə səma cismi qeydə alınıb. Süd Yolu qalaktikasının mərkəzində yerləşən superkütləli qara dəlik bizdən 26000 işıq ili uzaqlıqdadır.
Təbii ki, reallıqda qara dəliklər ən qarışıq şəkildə qarşımıza çıxır. Nəzəriyyədə isə sadələşdirilmiş modellərdən istifadə olunur. Sadələşdirilmiş olmasına baxmayaraq, real müşahidə olunan fiziki prosesləri izah etmək mümkündür. 4 belə sadələşdirilmiş qara dəlik modeli var:
1. Statik və yüksüz qara dəliklər ( Şvarzçild qara dəliyi)
2. Statik, yüklü qara dəliklər (Reisner-Nordstrom qara dəliyi)
3. Fırlanan yüksüz qara dəliklər (Kerr qara dəliyi)
4. Fırlanan və yüklü qara dəliklər (Kerr-Newman qara dəliyi)
Statik və yüksüz qara dəliklər
Adından da göründüyü kimi bu ən sadə və ən yaxşı öyrənilmiş modeldir. Fəzanın quruluşu M kütləli qara dəliklər üçün aşağıdakı formanı daşıyır:
Fəzanın xətt elementi, bu fəzanın iki qonşu nöqtəsi arasında məsafəni təyin edən əlaqədir. Yığcam şəkildə metrik tenzorla ifadə olunur.
Bu udulma və şüalanma prosesi enerjini çölə püskürdərək kütlə itirməsinə səbəb olur və Bekenstein-Hawking şüalanması adlanır. İlk dəfə Stephen Hawking göstərmişdir ki, bu şüalanmalar sonludur və müəyyən müddət ərzində qara dəlik tamamilə buxarlanacaq. Qara dəliyin yaşam müddəti onun kütləsinun kubu ilə düz mütənasibdir.
Burada, τ düzgün zaman, t Şvarzçild zamanı, rs Şvarzçild radiusu (rs = 2MG/c^2), c işıq sürəti, r, θ və φ isə koordinat nöqtələridir. Mərkəzdən r=rs Şvarçild məsafəsində yuxarıdakı tənlik təyin edilmir və həmin radiusda yerləşən çevrə hadisələr üfüqi adlanır. Bunun səbəbi, həmin nöqtədə baş verən hər bir şey uzaq kənardakı müşahidəçiyə görə sonsuz zamanda baş verir.
Müşahidəçilərimizi iki yerə ayıraq: Fidolar və frefolar. Fidolar fəzada sabit dayanmış, zamanı ölçən müşahidəçilər olsun. Frefolar isə bizimlə birgə sərbəst düşən müşahidəçilər olacaq.
Müşahidəçilərimizi iki yerə ayıraq: Fidolar və frefolar. Fidolar fəzada sabit dayanmış, zamanı ölçən müşahidəçilər olsun. Frefolar isə bizimlə birgə sərbəst düşən müşahidəçilər olacaq.
 |
| Qara dəliyə düşən zərrəciyin kənarda statik dayanan müşahidəçiyə nəzərən görünüşü |
Mərkəzdən uzaq məsafədən radial sərbəst düşən zərrəciyin yaşadıqlarını izah etməyə çalışaq. Fidolara görə bu zərrəcik hadisələr üfüqinə asimptotik yaxınlaşacaq. Eyni zamanda, zərrəciyin momenti fidonun zamanına exponensial şəkildə artacaq və Lorentz sıxılması baş verəcək. Sanki, zərrəcik üstdən sıxılıb kənarlara genişləyəcək. Frefonun özü isə təmiz fərqli hadisələr hiss edəcək.
Frefo sərbəst düşdüyü üçün heç bir qravitasiya effekti hiss etməyəcək. Fəzanın çökəkliyi də kiçik rəqəm olduğundan dartma qüvvəsi də hiss olunmayacaq qədər kiçik olacaq. Frefo üfüqü keçdikdən sonra fidolarla əlaqə qura bilməyəcək və kənardakı bütün müşahidəçilər üçün itmiş zənn ediləcək.
Sadə koordinat çevrilmələri ilə çevrilmiş fəzanın Minkovski fəzası olduğunu göstərmək olar. Minkovski fəzası bucaqların qorunduğu "uyğunlaşmış düz" fəzadır. Bu fəzanın görünən sərhədləri əslində real fəzamızda sonsuzla eynidir. Yəni, sonsuz fəzadan sonlu fəzaya keçirik və digər hesablamaları aparmaq daha asan olur. Hadisələr üfüqündən çöldəki hissəyə Rindler fəzası deyəcəyik. Uyğun Rindler zamanı əvvəlki Şvarçild zamanını əvəzləyəcək.
Rindler fəzasında kvant sahələrinin entropiyasını hesabladıqda ortaya gözəl nəticə çıxır. Belə ki, qara dəliyin termal entropiyası onun sahəsi ilə düz mütənasibdir. Termal dediyimizə görə qara dəlik ətrafında istilik var. Əslində, fidolara görə üfüq xəttinə yaxın yaranan virtual zərrəciklər heç də virtual deyil. Çünki, onlar qısa müddətə üfüq xəttini keçirlər. Amma, bu qısa müddət fidolar üçün sonsuz zaman deməkdir. Yəni, fidolar virtual zərrəciklərin bir-birini islah etdiyini görməyəcək. Beləliklə, qara dəliyin ətrafında nazik termik udulma və şüalanma proseslərinin baş verdiyi təbəqə yaranacaq (Unruh effekti). Təbii ki, yalnız fidolar üçün. Üfüq xəttini keçən frefo bu istiliyi hiss etməyəcək.
Frefo sərbəst düşdüyü üçün heç bir qravitasiya effekti hiss etməyəcək. Fəzanın çökəkliyi də kiçik rəqəm olduğundan dartma qüvvəsi də hiss olunmayacaq qədər kiçik olacaq. Frefo üfüqü keçdikdən sonra fidolarla əlaqə qura bilməyəcək və kənardakı bütün müşahidəçilər üçün itmiş zənn ediləcək.
Sadə koordinat çevrilmələri ilə çevrilmiş fəzanın Minkovski fəzası olduğunu göstərmək olar. Minkovski fəzası bucaqların qorunduğu "uyğunlaşmış düz" fəzadır. Bu fəzanın görünən sərhədləri əslində real fəzamızda sonsuzla eynidir. Yəni, sonsuz fəzadan sonlu fəzaya keçirik və digər hesablamaları aparmaq daha asan olur. Hadisələr üfüqündən çöldəki hissəyə Rindler fəzası deyəcəyik. Uyğun Rindler zamanı əvvəlki Şvarçild zamanını əvəzləyəcək.
Rindler fəzasında kvant sahələrinin entropiyasını hesabladıqda ortaya gözəl nəticə çıxır. Belə ki, qara dəliyin termal entropiyası onun sahəsi ilə düz mütənasibdir. Termal dediyimizə görə qara dəlik ətrafında istilik var. Əslində, fidolara görə üfüq xəttinə yaxın yaranan virtual zərrəciklər heç də virtual deyil. Çünki, onlar qısa müddətə üfüq xəttini keçirlər. Amma, bu qısa müddət fidolar üçün sonsuz zaman deməkdir. Yəni, fidolar virtual zərrəciklərin bir-birini islah etdiyini görməyəcək. Beləliklə, qara dəliyin ətrafında nazik termik udulma və şüalanma proseslərinin baş verdiyi təbəqə yaranacaq (Unruh effekti). Təbii ki, yalnız fidolar üçün. Üfüq xəttini keçən frefo bu istiliyi hiss etməyəcək.
Bu udulma və şüalanma prosesi enerjini çölə püskürdərək kütlə itirməsinə səbəb olur və Bekenstein-Hawking şüalanması adlanır. İlk dəfə Stephen Hawking göstərmişdir ki, bu şüalanmalar sonludur və müəyyən müddət ərzində qara dəlik tamamilə buxarlanacaq. Qara dəliyin yaşam müddəti onun kütləsinun kubu ilə düz mütənasibdir.
Statik və yüklü qara dəliklər
Elektrostatik yükə malik fırlanmayan qara dəliklər üçün xətt elementi daha qəlizdir:
Burada əlavə olaraq rq = Q^2*G/(4πε0c^4) kəmiyyəti var ki, Q yükünün yaratdığı əlavə yük momentidir. Sonuncu hədd isə əvvəlki ifadədəki bucaqlardan asılı hissəni əvəz edir. Q^2 > M^2 G olduğu halda əlavə sinqulyarlıq meydana çıxır. Bu sinqulyarlıq əvvəlkindən fərqli olaraq kənardan müşahidə edilə biləndir. Klassik nisbilik nəzəriyyəsinə bu zidddir. Bərabərlik halına ekstremal qara dəliklər adı verilib. Ümumiyyətlə, yüklü qara dəliklərin iki üfüqü olur: daxili və xarici. Oxşar qaydada Rindler fəzasına keçid edərək yuxarıda sözügedən prosesləri analiz etmək olar. Məlum olur ki, yüklü qara dəliklər buxarlanaraq tamam yox olmurlar, bilinən sükunət halında buxarlanma prosesi dayanır.
Fırlanan yüklü və yüksüz qara dəliklər
Fırlanan qara dəliklər dedikdə sabit bucaq momentinə sahib olmaları nəzərdə tutulur. Belə olan halda xətt elementi daha da qəliz forma alır. Ümumiləşdirilmiş Kerr-Newman qara dəliyi üçün
Burada J bucaq momentidir.
Göründüyü kimi xətt elementi olduqca qəlizdir. Dəqiq hesablamalar aparmaq çox çətindir. Buna görə də lazımi yaxınlaşmalar edilib Rindler fəzasını almaq kifayətdir ki, əvvəlki mülahizələri bu tip qara dəliklər üçün də aparaq.

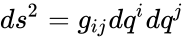




2 Comments
Bucaqların qorunduğu, sərhədli fəza Minkowski fəzası deyil axı. Bu xüsusiyyətlər Penrose diaqramına aiddir, elə deyil?
ReplyDeleteBucaqların qorunduğu, sərhədli fəzalar Minkovski metriki ilə göstərilir. Penrose diaqramları da Minkovski fəzası üzərində göstərilir.
Delete